Primero que nada para hablar de este tema se tiene que tener un concepto de que es la lógica proposicional.
La lógica proposicional es la parte de la lógica que estudia la formación de proposiciones complejas a partir de proposiciones simples, y la inferencia de proposiciones a partir de proposiciones, pero sin tener en cuenta la estructura interna de las proposiciones más simples.
Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
La proposición es el significado de una idea, enunciado,conjunto de palabras o letras a las que se les puede asignar uno y sólo uno de los valores de verdad, que pueden ser:
VERDADERO (V) o FALSO(F)
Por lo general, a las proposiciones se las representa por las letras del alfabeto desde la letra p, es decir, p, q, r, s, t, ... etc. Así, por ejemplo, podemos citar las siguientes proposiciones y su valor de verdad:
p : 15 + 5 = 21 (F)
q: Santa Fe es una provincia Argentina. (V)
r: El número 15 es divisible por 3. (V)
s: El perro es un ave. (F)
Existe una notacion para trabajar con ellas y es esta:
Notación y Conectivos Lógicos
A partir de proposiciones simples es posible generar otras, simples o compuestas. Es decir que se puede operar con proposiciones, y para ello se utilizan ciertos símbolos llamados conectivos lógicos. A continuación vemos una concreta definición de cada uno:
|
APLICACIÓN DE LA LÓGICA PROPOSICIONAL
La lógica proposicional dio origen a la algebra booleana que esta a su vez fue la base para la informatica y para la forma en que funcinarion los primeros ordenadores. Ya que el algebra de boole es el area de las matematicas que se aplica en el diseño de circuitos logicos .
Debido a que los computadores trabajan con información binaria, la herramienta matemática adecuada para el análisis y diseño de su funcionamiento es el Álgebra de Boole. El Álgebra de Boole fue desarrollada inicialmente para el estudio de la lógica. Ha sido a partir de 1938, fecha en que Claude Shannon publicó un libro llamado "Análisis simbólico de circuitos con relés", estableciendo los primeros conceptos de la actual teoría de la conmutación, cuando se ha producido un aumento considerable en el número de trabajos de aplicación del Álgebra de Boole a los computadores digitales. Hoy en día, esta herramienta resulta fundamental para el desarrollo de los computadores ya que, con su ayuda, el análisis y síntesis de combinaciones complejas de circuitos lógicospuede realizarse con rapidez.
Ya que se puede aplicar de este modo.
La verdad de una proposición puede asociarse al pasaje de corriente en un circuito eléctrico con un interruptor.
Así, para representar a p, si es F, se tiene

y para p, si es V, se tiene:

Es decir, el interruptor se cierra si p es V y se abre si p es F.
Podemos, así, representar las operaciones proposicionales mediante circuitos con tantos interruptores como proposiciones componentes, combinados en serie o paralelamente.
Veremos, a continuación, como representar en forma booleana las operaciones que surgen de operar con dos proposiciones mediante los conectivos lógicos que conocemos
Conjuncion

Este circuito admite el pasaje de corriente, es decir la verdad de p^q , solo si ambas son V .
Disyuncion
Está representada por un circuito en paralelo.

Como vemos, admite el pasaje de corriente cuando al menos una de las dos es V (comprobar en la correspondiente tabla de verdad).


Cuando se trabaja con circuitos digitales es muy común que al final de un diseño se tenga un circuito con un número de partes (circuitos integrados y otros) mayor al necesario.
Para lograr que el circuito tenga la cantidad de partes correcta (la menor posible) hay que optimizarlo (reducirlo).
Un diseño óptimo causará que:
- El circuito electrónico sea más simple
- El número de componentes sea el menor
- El precio de proyecto sea el más bajo
- La demanda de potencia del circuito sea menor
- El mantenimiento del circuito sea más fácil.
- Es espacio necesario (en el circuito impreso) para la implementación del circuito será menor.
En consecuencia que el diseño sea el más económico posible.
Una herramienta para reducir las expresiones lógicas de circuitos digitales es la matemáticas de expresiones lógicas, que fue presentada por George Boole en 1854,herramienta que desde entonces se conoce como álgebra de Boole.
Las reglas del álgebra Booleana son:
Notas:
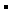 (punto): significa producto lógico. + (signo de suma): significa suma lógica
(punto): significa producto lógico. + (signo de suma): significa suma lógicaOperaciones básicas en el algebra booleana

Ley Distributiva, ley Asociativa, ley Conmutativa



Precedencia y Teorema de Morgan


Para asegurarse de que la reducción del circuito electrónico fue exitosa, se puede utilizar la tabla de verdad que debe dar el mismo resultado para el circuito simplificado y el original.

Y esa es una aplicación que tiene la lógica proposicional , que se utiliza en el diseño de circuitos.
Referencias:
http://www.unicrom.com/dig_algebra_booleana.asp
http://es.wikipedia.org/wiki/L%C3%B3gica_proposicional
http://soko.com.ar/matem/Logica_proposicional.htm
















 .
.







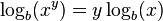
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](http://upload.wikimedia.org/wikipedia/es/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](http://upload.wikimedia.org/wikipedia/es/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)
