La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base aque utilicen.
Definicion Formal
La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base aque utilicen.
Propiedades
La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.
- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
- su límite en - ∞ es 0, y en + ∞ es + ∞
Como derivarla
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,
Es decir, ex es su propia derivada . Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:
- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial
 .
.
Si la base de la exponencial no es el número e, sino otro número real arbitrario a mayor que 0, entonces la derivada de ésta es:
donde la función ln denota el logaritmo natural.
Aquí unos ejemplos de la Derivada de la función exponencial de base e
La derivada de la función exponencial de base e es igual a la misma función
por la derivada del exponente.
Ejemplos



La integral de una exponencial es de esta formula :
Y qui algunos ejemplos:

Logarítmicas
En matemáticas, el logaritmo de un número —en una base determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la potenciación de la base del logaritmo.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron rápidamente adoptados por científicos, ingenieros, y otros para realizar operaciones más fácilmente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante — por derecho propio — que el logaritmo de un producto es la suma de los logaritmos de los factores:
Los logaritmos, independientemente de la base elegida, cumplen una serie de propiedades comunes que los caracterizan. Así, logaritmo de su base es siempre 1; logb b = 1 ya que b1 = b. El logaritmo de 1 es cero (independientemente de la base); logb 1=0 ya que b0 = 1.
Si el número real a se encuentra dentro del intervalo 0 < a < 1 entonces logb a da un valor negativo o se dice que es un logaritmo negativo. Es evidente, ya que si logaritmo de 1 es cero, entonces valores reales menores que uno serán negativos por ser la función logarítmica estrictamente creciente y cuyo recorrido es (-∞, +∞). También se puede demostrar usando la identidad logarítmica logb(x/y)=logb x - logb y; puesto que a pertenece al intervalo 0 < a < 1, su inverso a-1 será mayor que uno, con lo que logb(a)=logb(1/a-1) = logb 1 - logb(a-1)= -logb(a-1).
Los números negativos no tienen logaritmo en el cuerpo de los reales R, ya que cualesquiera que sea el exponente n, se tendrá siempre que bn será mayor que cero, bn > 0; en consecuencia, no hay ningún valor real de n que pueda satisfacer bn = x cuando x sea menor que 0. Sin embargo, este obstáculo se puede salvar, ampliando el dominio de definición al cuerpo de los números complejos C, pudiendo calcular logaritmos de números negativos usando el logaritmo complejo o recurriendo a la fórmula de Euler.
Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Por ejemplo, las potencias de 2 son 1,2,4,8,16,32,64...etc y sus exponentes serán 0, 1, 2, 3, 4... etc ya que 20 = 1, 21 = 2, 22 = 4, 23 = 8, y 24 = 16 etc. luego log2 1 = 0, log2 2 = 1, log2 4 = 2, log2 8 = 3 y log2 16 = 4 etc.
Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:
-
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](http://upload.wikimedia.org/wikipedia/es/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)
Derivada de un logaritmo
 Como
Como , también se puede expresar así:
, también se puede expresar así:
Derivada de un logaritmo neperiano

Ejemplos de derivadas logarítmicas


 Aplicando las propiedades de los logaritmos tenemos:
Aplicando las propiedades de los logaritmos tenemos:


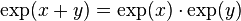
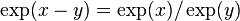







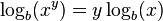
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](http://upload.wikimedia.org/wikipedia/es/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
Quizá unas gráficas y un estilo más consistente de las ecuaciones... Van 14 pts. No olvides incluir bibliografía.
ResponderEliminar