Funcion Sigmoidal

Función sigmoidal o logística
Es probablemente la función de activación más empleada en la actualidad.



Se trata de una función continua no lineal con bastante plausibilidad fisiológica.La función sigmoidal posee un rango comprendido entre 0 y 1. Esto, aplicado a las unidades de proceso de una red neuronal artificial significa que, sea cual sea la entrada, la salida estará comprendida entre 0 y1.
Esta función depende del parámetro s , que usualmente toma el valor 1.

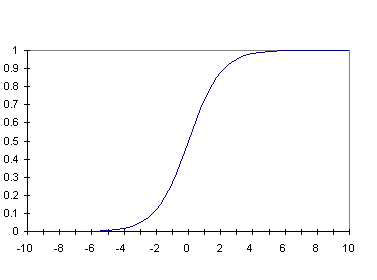
Ilustración 7: Función sigmoidal con s = 1
La salida de una unidad vale 0.5 cuando la entrada es nula, esto significa que la unidad tiene cierta actividad aún en ausencia de estimulación. Al aumentar la estimulación la unidad aumenta su activación, y la disminuye si la estimulación es inhibitoria, de forma parecida a como se comportan las neuronas reales.
Presenta las siguientes características deseables .

1. Acomodación de señales muy intensas sin producir saturación.
2. Admite señales débiles sin excesiva atenuación
3. Fácilmente derivable, ya que 

La principal limitación de esta función es que no sirve para expresar polaridades, da siempre valores positivos. Una función alternativa con cualidades parecidas pero con un rango entre -1 y 1 es la función tangente hiperbólica. Desde un punto de vista fisiológico, el signo negativo se puede interpretar como una disminución de la tasa de disparo de una neurona por debajo de la tasa de disparo en reposo.

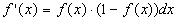
 Funcion Sigmoidal Echa en clase

 Utilizando la terminal escribe gutplot y ya se podra directamente escribir la formula que deseas y moviendo los valores .

Basta con escribir plot 1.0/(1.0*exp(-x/0.2))

para que nos genere una grafica como esta.

 Como les mencione puedes estar variando los valores y aqui dandole otro valor se obtiene esta otra grafica.